Merge Two Sorted Arrays
Problem Statement
1Problem Description :2Given two integer arrays A and B sorted in increasing order, merge A and B into a single sorted array C in increasing order.34Input:5Two sorted arrays A and B67Output:8Return merged sorted array C.
Solution Approaches
Naïve Solution
Prerequisite
Algorithm
- Create an array C of length m+n where m is length of array A and n is length of array B.
- Copy elements of A and B into Array C.
- Sort the array C.
Complexity Analysis
- Time Complexity : O( (m+n) log (m+n) ) (Sorting Complexity)
- Space Complexity: O(1)
Using Two Pointers
Prerequisite
Algorithm
1Input : Sorted arrays A and B given23Step 1: Initialize m and n to length of the arrays A and B respectively.45Step 2: Create empty array C of length m+n.67Step 3: initialize i, j and k to index 0 of A, B and C respectively.89Step 4: if i < m and j < n , compare A[i] and B[j]10 Step 4.1 : if A[i] is lesser than B[j], copy A[i] into C[k] and increment i and k.11 Step 4.2 : else copy B[j] into C[k] and increment j and k.1213Step 5: else if i < m copy A[i] into C[k] and increment i and k.1415Step 6: else if j < n copy B[j] into C[k] and increment j and k.1617Step 7: Repeat Steps 4 to 6 until we exhaust arrays A and B.
Example Dry Run
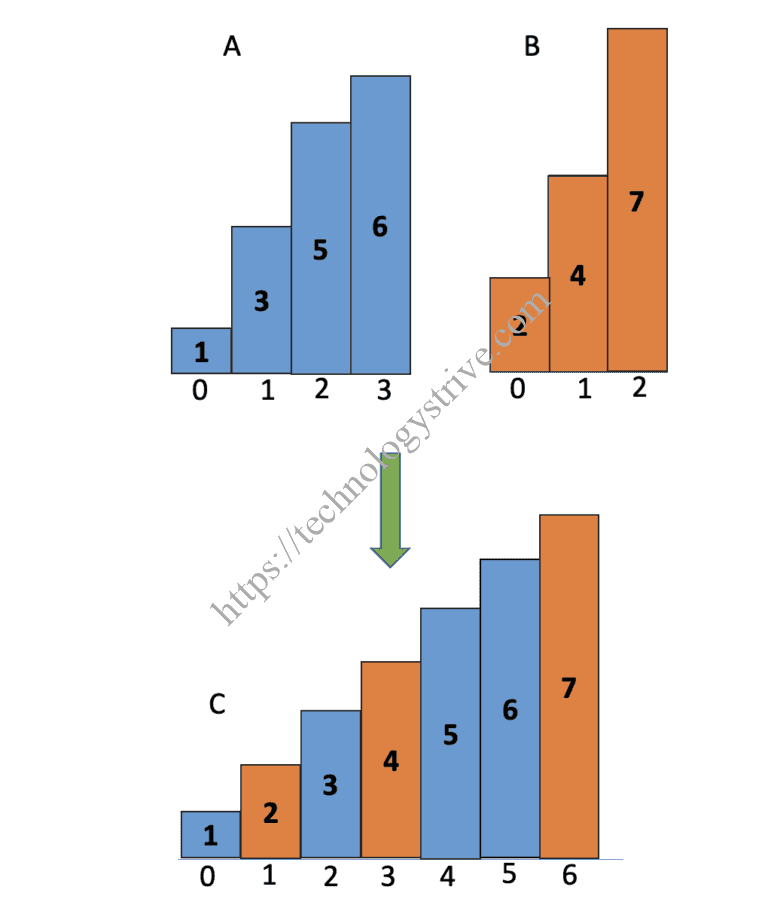
Input : A[] = {1, 3, 5, 6} , B[] = {2, 4, 7}
1Step 1 : m = A.length and n = B.length => A = 4 and B = 323Step 2: initialize result array C of length (m+n) which is 745Step 3 : initialize i = 0 , j = 0 and k = 0 for arrays A, B and C respectively.67Step 4 to 68 Iteration 1 : i = 0, j = 0 and k = 09 Compare A[0] with B[0]10 here A[0] < B[0] => C[0] = A[0] and i ++, k++1112 Iteration 2 : i = 1, j = 0 and k = 113 Compare A[1] with B[0]14 here A[1] > B[0] => C[1] = B[0] and j++, k++1516 Iteration 3 : i = 1, j = 1 and k = 217 Compare A[1] with B[1]18 here A[1] < B[1] => C[2] = A[1] and i++, k++1920 Iteration 4 : i = 2, j = 1 and k = 321 Compare A[2] with B[1]22 here A[2] > B[1] => C[3] = B[1] and j++, k++2324 Iteration 5 : i = 2, j = 2 and k = 425 Compare A[2] with B[2]26 here A[2] < B[2] => C[4] = A[2] and i++, k++2728 Iteration 6 : i = 3 and j = 2 and k = 529 Compare A[3] with B[2]30 here A[3] < B[2] => C[5] = A[3] and i++, k++3132 Iteration 7: i = 4 and j = 2 and k = 633 As A elements over C[6] = B[2] and j++3435Both A and B elements exhausted and we got the final array C.
Output : {1, 2, 3, 4, 5, 6, 7}
Java Implementation
1import java.util.Arrays;2public class MergeTwoSortedArrays {34 public int[] merge(int[] A, int[] B) {5 // initialize m and n to length of arrays A and B6 int m = A.length;7 int n = B.length;89 // create result array C of length (m+n)10 int[] C = new int[m+n] ;1112 // initialize i, j and k to 013 // Index i is for array A14 // Index j is for array B15 // Index k is for result array C16 int i=0 , j = 0, k = 0;1718 //Condition to check any array got exhausted ?19 while(i < m && j < n){2021 // compare A[i] with B[j]22 if(A[i] < B[j]){2324 // As A[i] is smaller, copy A[i] into C[k]25 C[k] = A[i];2627 // as A[i] processed move to next element by incrementing i28 // as C[k] already filled, move to next index by incrementing k29 i++; k++;30 }else{3132 // As B[j] is smaller, copy B[j] into C[k]33 C[k] = B[j];3435 // as B[j] processed move to next element by incrementing j36 // as C[k] already filled, move to next index by incrementing k37 j++; k++;38 }39 }4041 // This is the case when array B all elements processed &42 // A has still unvisited elements43 while(i < m) {44 C[k++] = A[i++];45 }4647 // This is the case when array A all elements processed &48 // B has still unvisited elements49 while (j < n) {50 C[k++] = B[j++];51 }5253 // return the result array54 return C;55 }5657 // Driver Code to test the code58 public static void main(String[] args) {59 MergeTwoSortedArrays obj = new MergeTwoSortedArrays();60 int[] A = {1, 3, 5, 6};61 int[] B = {2, 4, 7};62 int[] resultArray = obj.merge(A, B);63 System.out.println(Arrays.toString(resultArray));64 }65}
Complexity Analysis
- Time Complexity : O(m+n) where m and n are length of arrays A and B respectively.
- Space Complexity: O(1) as we are not using any extra space.
Approaches Comparison
| Approach | Time Complexity | Space Complexity | Remarks |
|---|---|---|---|
| Naïve Solution | O( (m+n) log (m+n) ) | O(1) | Complexity of Sorting the array |
| Using Two Pointer Technique | O(m+n) | O(1) |