Introduction

Searching is the process of finding a desired element from a collection of available elements. For example, searching for a particular contact number in a phone directory. Desired phone number is called target and the phone directory is called search space. Search algorithms designed to find whether the target exists in the search space or anything. The search space can be an array or a list or it can be a database.

To understand searching algorithms in clear, let us consider the search space is an array “a” which contains “n” elements and the desired element or target element which we want to search is “k”.

In Binary Search, we compare the target element with the middle element of the given sorted array and based on the outcome, we further divide the array into half and continue until we find the given element. If we find the given target element in the array, the search is successful, else the search process is unsuccessful. Binary Search is an efficient searching algorithm compared to Linear Search and is widely used in many applications. To apply Binary Search the search space should maintain some ordering, incase of linear search there is no need of maintaining the order between the elements.

In real life we use binary search algorithms in many problems without realizing it. For Instance, we have a book which has 1000 pages and if we want to open page number 567, we first try to open some random page and we check the current page number. By looking at the current page number, we try to discard either left side or right side and we continue our search process for remaining pages. If we have to implement the same in computer science, instead of using random search, we always search by picking the middle element of the search space and discard exactly half of the elements of the search space. We continue the same process until we find the target element or there are no elements left in the search space.

Algorithm

1Input  : Array a[] of length n and k is the target element 
2Step 1 : Set index low to 0, high to n-1 
3Step 2 : If low > high return -1 (Search Process is not successful) 
4Step 3 : Compute mid of the array as mid = (low+high)/2  
5Step 4 : Else a[mid] == k satisfies so return mid (Search Process is successful) 
6Step 5 : If a[mid] > k , set high = mid-1 and goto step 2 
7Step 6 : Else if a[mid] < k set low = mid+1 and goto step 2 

Explanation

Let us understand the binary search algorithm using an example with dry run.

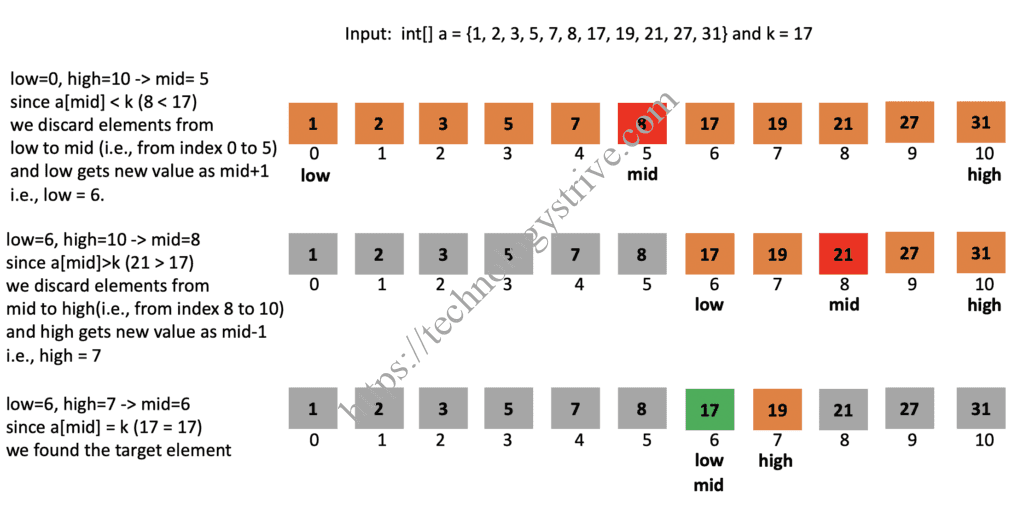
1Input  : int[] a = {1, 2, 3, 5, 7, 8, 17, 19, 21, 27, 31} and k = 17
2Output : 6

1 Iteration1 : 
2   Step1 : Initialize low = 0 high = 10 (as length of the array is 11) 
3   Step2 : low <= high (0 <= 10)satisfies so proceed with step3 
4   Step3 : mid = (low+high)/2 = (0+10)/2 = 5 
5   Step4 : check a[mid] is equal to k or not, 
6           here a[mid] = 8 and k = 17 and 8 ≠ 17, so goto step5 
7   Step5 : check a[mid] > k, 
8           here a[mid] = 8, k = 17 and 8 > 17 not satisfies, so goto step6 
9   Step6 : check a[mid] < k, 
10           here a[mid] = 8, k = 17 and 8 < 17 satisfies, 
11           as low = mid+1 = 6 and repeat step2 
12 
13 Iteration 2: 
14   Step2 : low <= high (6<10) satisfies, so goto step3 
15   Step3 : mid = (low+high)/2 = (6+10)/2 = 8  
16   Step4 : check a[mid] is equal to k or not, 
17           here a[mid] = 21, k=17 and 21 ≠ 17, so goto step5 
18   Step5 : check a[mid] > k, 
19           here a[mid] = 21, k = 17 and 21 > 17 satisfies,  
20           as high = mid-1 = 7 and repeat step2 
21
22 Iteration 3: 
23   Step2 : low <= high (6 <= 7) satisfies so proceed with step3 
24   Step3 : mid = (low+high)/2 = (6+7)/2 = 6 
25   Step4 : check whether a[mid] is equal to k or not, here a[mid] = k satisfies, 
26           Search process gets terminated here and returns mid index which is 6. 

Iterative Implementation

1public class BinarySearch {
2
3    // Method to search for given value k in an array
4    public int search(int[] a, int k) {
5        // initialize low to 0 and high to n-1
6        int low = 0;
7        int high = a.length - 1;
8
9        // loop until the search space is exhausted 
10        // by checking with middle element
11        while (low <= high) {
12            // compute middle index of the array
13            int mid = (low + high) / 2;
14
15            // compare a[mid] with k (target value),
16            if (a[mid] == k) {
17                // As target found return mid
18                return mid;
19            }
20
21            // if middle element is lesser than target element
22            // discard all elements left to middle(including middle element)
23            if (a[mid] < k) {
24                low = mid + 1;
25            }
26
27            // if middle element is greater than target element
28            // discard all elements right to middle(including middle element)
29            else {
30                high = mid - 1;
31            }
32        }
33        // No match found, so return -1.
34        return -1;
35    }
36
37    public static void main(String[] args) {
38        // search space
39        int[] a = {1, 2, 3, 5, 7, 8, 17, 19, 21, 27, 31};
40
41        // target element
42        int k = 17;
43
44        int index = new BinarySearch().search(a, k);
45        if (index == -1) {
46            System.out.println("Target element is not found");
47        } else {
48            System.out.println("Target element found at index " + index);
49        }
50    }
51}

Recursive Implementation

1public class BinarySearchRecursive {
2
3    // Method to search for given value k in an array
4    public int search(int[] a, int k){
5        // initialize search space using low and high variables
6        // initialize low as 0 and high to last index of the array
7        int low = 0;
8        int high = a.length-1;
9        return search(a, k, low, high);
10    }
11
12    // recursive implementation for binary search algorithm
13    public int search(int[] a, int k, int low, int high){
14
15        // when no elements left in the search space
16        if(low>high){
17            return -1;
18        }
19
20        // computer middle index of the search space
21        int mid = (low+high)/2;
22
23        // compare a[mid] with k (target value)
24        if(a[mid] == k){
25            // As target found return mid
26            return mid;
27        }
28
29        // if middle element is lesser than target element
30        // discard all elements left to middle(including middle element)
31        if(a[mid] < k){
32
33            // continue search process for new search space
34            return search(a, k, mid+1, high);
35        }
36
37        // if middle element is greater than target element
38        // discard all elements right to middle(including middle element)
39        // continue search process for new search space
40        return search(a, k, low, mid-1);
41    }
42
43    public static void main(String[] args) {
44        // search space
45        int[] a = {1, 2, 3, 5, 7, 8, 17, 19, 21, 27, 31};
46
47        // target element
48        int k = 17;
49
50        int index = new BinarySearch().search(a, k);
51        if (index == -1) {
52            System.out.println("Target element is not found");
53        } else {
54            System.out.println("Target element found at index " + index);
55        }
56    }
57}

Complexity Analysis

Time Complexity Analysis

In Binary Search, at every iteration we exactly discard half of the elements and continue the search process with the remaining half until we find the target element or there are no elements left in the search space. Each iteration search space becomes exactly half of its size, for example if search space contains n elements

Iteration 1 : (n/2) = n/2^1

Iteration 2 : (n/2)/2 =(n/4) = n/2^2

Iteration 3 : (n/4)/2 =(n/8) = n/2^3

This process terminates when we have one element left in the array and assume the iteration number as k

Iteration k: n/2^k = 1 => k =log2(n)

Time Complexity = log2(n) where n is the number of elements in the search space.

Space Complexity Analysis

Space Complexity of binary search algorithm depends on the way we implement (iterative or recursive)

In iterative implementation, there is no extra auxiliary space used, so space complexity is O(1). In recursive implementation, on average recursive call gets triggered log2(n), that means it uses log2(n) stack space for recursive calls, so space complexity is log2(n).