Introduction

Searching is the process of finding a desired element from a collection of available elements. For example, searching for a particular contact number in a phone directory. Desired phone number is called target and the phone directory is called search space. Search algorithms designed to find whether the target exists in the search space or anything. The search space can be an array or a list or it can be a database.

To understand searching algorithms in clear, let us consider the search space is an array "a" which contains "n" elements and the desired element or target element which we want to search is "k".

In Linear Search, we traverse the array sequentially to and check if the element is matching with the given target element or not. If we find any element in the array that matches with the target element then the search process is successful and we return the index of the element in the array. If we don’t find any matching element in the array, the search process is unsuccessful and we return -1.

Algorithm

1Input  : Array a[] of length n and k is the target element 
2Step 1 : Set index i to 0 (start index) 
3Step 2 : If i >= n return -1 (We reached end of the array and search is unsuccessful) 
4Step 3 : If a[i] is equal to k,  return i (search process is successful) 
5Step 4 : Else increase i by 1 
6Step 5 : Repeat Step2 (As still elements left in the array to compare)

Example

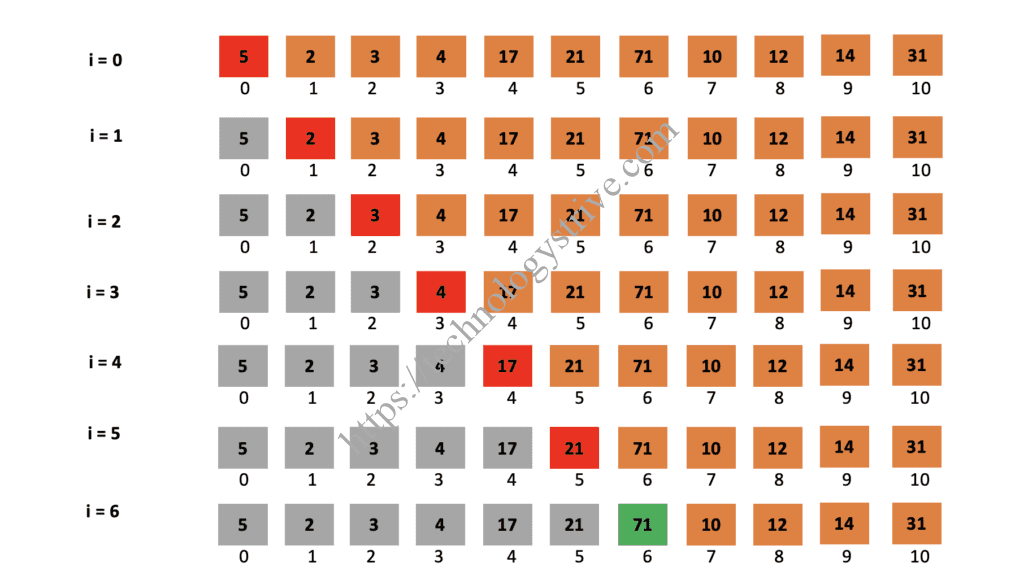
Let us understand the linear search algorithm using an example with dry run.

1Input:  int[] a = {5, 2, 3, 4, 17, 21, 71, 10, 12, 14, 31} and k = 71
2output: 6

Code Implementation

1public class LinearSearch {
2
3    // Method to search for given value k in an array
4    public int search(int[] a, int k) {
5        // loop through elements of array
6        for (int i = 0; i < a.length; i++) {
7            // Check the current element matching with target element
8            // Match found, so return index of the element
9            if (a[i] == k) {
10                return i;
11            }
12        }
13        // No match found, so return -1.
14        return -1;
15    }
16
17    public static void main(String[] args) {
18        // search space
19        int[] a = {5, 2, 3, 4, 17, 21, 71, 10, 12, 14, 31};
20        // target element
21        int k = 71;
22
23        int index = new LinearSearch().search(a, k);
24        if (index == -1) {
25            System.out.println("Target element is not found");
26        } else {
27            System.out.println("Target element found at index " + index);
28        }
29    }
30}

Video Explanation

Complexity Analysis

Time Complexity

Best Case : O(1) If the first element of the array is matching with the target element , just in one comparison the search process gets successful and so time complexity will be O(1)

Worst Case : O(n) As there are n elements in the array, there might be a possibility that the target element might be at the end of the array or the target element does not exist in the given array. In both cases a total of n comparisons needed to get the search process to be completed. So time complexity in the worst case will be O(n).

Space Complexity

We don’t need any extra process during the process of the search algorithm. So space complexity will be O(1).