Introduction

Bubble Sort is the easiest sorting algorithm in which adjacent elements are compared with each other and swapped if the elements are not in proper order. This process repeatedly scans the elements of the list and each iteration one element will be placed at the correct position starting with the first max element, second max element and so on.

Algorithm

1Step 0 : Initialize n to length of the array 
2
3Step 1 : Initialize j to 0 and compare a[j] with a[j+1] 
4         (Compare adjacent elements starting from 0th index) 
5
6Step 2 : if a[j] > a[j+1] swap a[j] and a[j+1] 
7
8Step 3 : repeat steps 1 and 2 until j reached end of the array 
9         (By end of this one element will be placed at its correct order) 
10
11Step 4 : continue from Step 1 n-1 times 
12         (So that all elements will be in proper order) 

Example Explanation

Input array : a = [5, 3, 13, 2, 11, 4, 7]

Iteration 1 :

Step 1 : Initialize j = 0 & compare first element (a[0]) and second element (a[1])

Step 2 : As a[j] > a[j+1] , swap a[j] and a[j+1]

Step 3 : Increment j and continue Step 2 until we reach the end of the array.

At the end of iteration 1, the max element will be placed at the last index of the array. We continue the same process n-1 times for the remaining unsorted array.

Iteration 2 :

Iteration 3 :

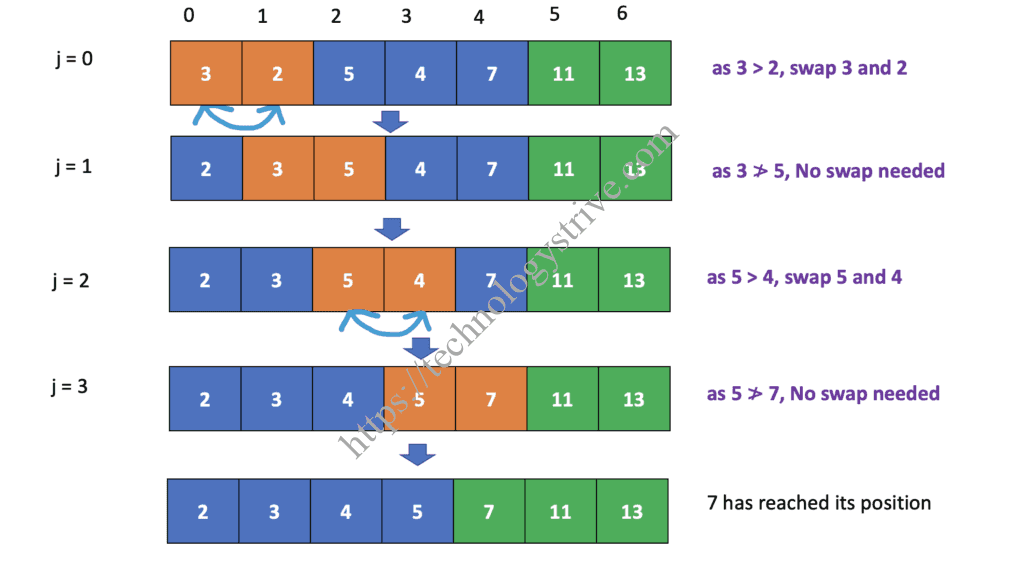
Iteration 4 :

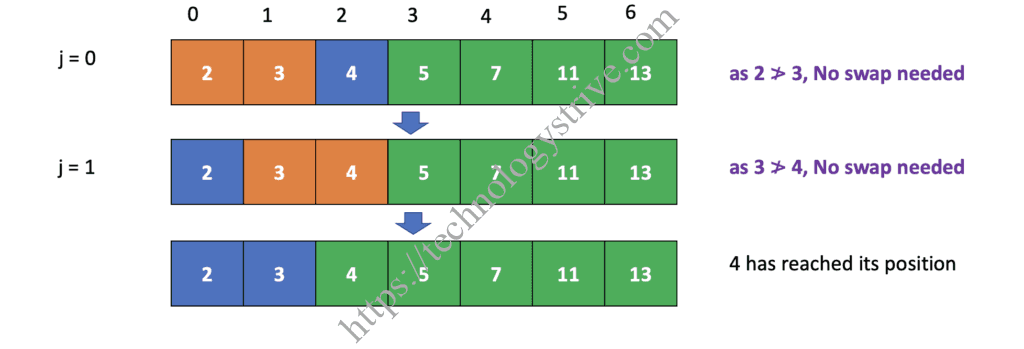
Iteration 5 :

Iteration 6 :

Code Implementation

1public class BubbleSort {
2
3    // Method to sort a given array
4    public void sort(int[] array){
5        int n = array.length;
6
7        //loop through elements of the array
8        for(int i=0;i<n-1;i++){
9
10            // loop to compare elements of the array
11            for(int j=0;j<n-i-1;j++){
12
13                // compare adjacent elements
14                if(array[j] > array[j+1]){
15                    
16                    // if adjacent elements are not in sorted order
17                    // swap the elements
18                    swap(array, j, j+1);
19                }
20            }
21        }
22    }
23
24    // method to swap elements in an array
25    private void swap(int[] array, int i, int j){
26        int temp = array[i];
27        array[i] = array[j];
28        array[j] = temp;
29    }
30
31    // Helper method to print an array
32    private void print(int[] array) {
33        for(int i=0; i<array.length; i++) {
34            System.out.print(array[i]+"\t");
35        }
36        System.out.println();
37    }
38
39    // Driver Code
40    public static void main(String[] args){
41        int[] a = {5, 3, 13, 2, 11, 4, 7};
42        BubbleSort obj = new BubbleSort();
43        obj.print(a);
44        obj.sort(a);
45        obj.print(a);
46    }
47
48}

Optimized Bubble Sort

Observation

As per the explanation given for an example, if we notice at the end of iteration 3, the array is fully sorted, and during 4th iteration there are no swap operations performed, by using this observation we can stop further scans to optimize the bubble sort algorithm. Using this optimized technique we will achieve O(n) time complexity in the best case (Input array is already in sorted order).

Implementation

1public class BubbleSortOptimized {
2
3    // Method to sort the given array
4    public void sort(int[] array) {
5        int n = array.length;
6
7        // Iterate through elements of array
8        for(int i=0;i<n-1;i++) {
9
10            // use flag swapped to check occurrence of swap operation
11            boolean swapped = false;
12
13            // loop through array
14            // compare adjacent elements of the array
15            for(int j=0;j<n-i-1;j++) {
16
17                if(array[j] > array[j+1]) {
18
19                    swap(array, j, j + 1);
20                    
21                    // update swapped to true
22                    swapped = true;
23                }
24            }
25            // no swapping happened entire array
26            // it means array is already in sorted order
27            if(!swapped) {
28               return;
29            }
30        }
31    }
32
33    // Helper method to swap two elements in the array
34    private void swap(int[] array, int i, int j) {
35        int temp = array[i];
36        array[i] = array[j];
37        array[j] = temp;
38    }
39
40    // Helper method to print an array
41    private void print(int[] array) {
42        for(int i=0; i<array.length; i++) {
43            System.out.print(array[i]+"\t");
44        }
45        System.out.println();
46    }
47
48    // Driver Method
49    public static void main(String[] args){
50        int[] a = {5, 3, 13, 2, 11, 4, 7};
51        BubbleSortOptimized obj = new BubbleSortOptimized();
52        obj.print(a);
53        obj.sort(a);
54        obj.print(a);
55    }
56}

Complexity Analysis

Time Complexity :

• Best Case : O(n)
• Worst Case : O(n^2)

Space Complexity : O(1).