Introduction

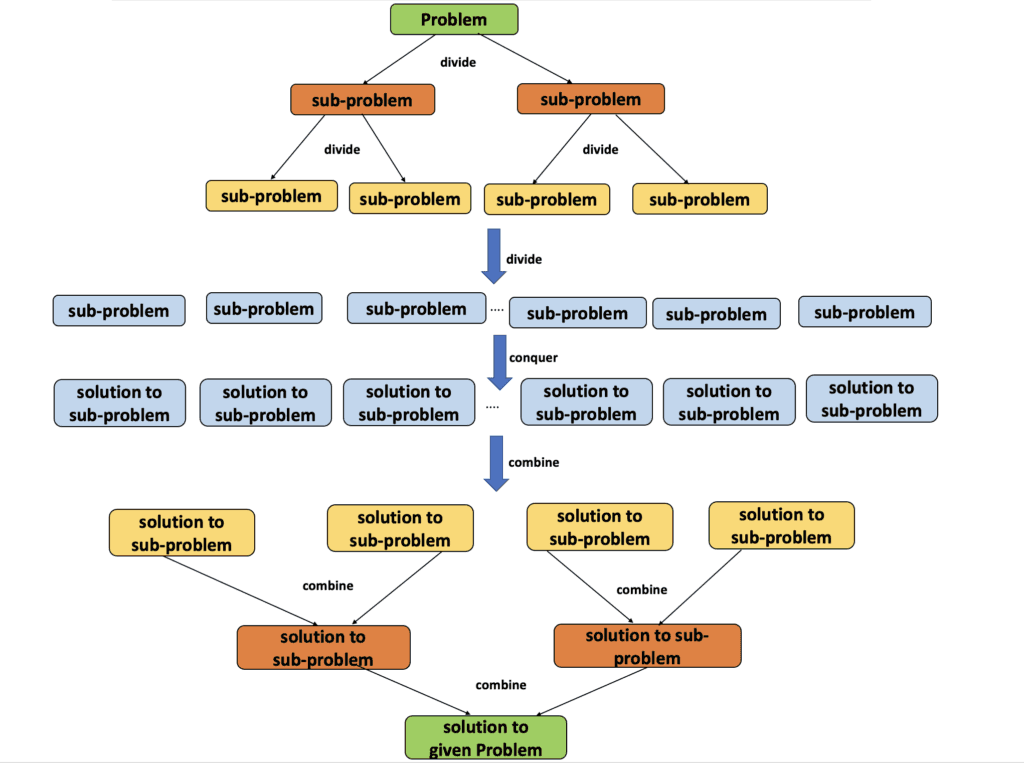
Divide and conquer is an algorithmic design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub problems are then combined to give a solution to the original problem.

Divide and Conquer algorithm is a recursive problem solving approach in which

• Given problem is divided into smaller sub problems
• Solving the smaller sub problems
• Combining the results of smaller sub problems

For example, to sort a given array of n integers, split the array into two arrays of about n/2 size each, sort each of them in turn, and interleave both results appropriately to obtain the sorted version of the given array. This approach is known as the merge sort algorithm.

Algorithm

• Divide : Dividing the problem into smaller sub problems which are similar to the original problem. The sub problem is further divided into sub problems and this process continues until the sub problem is easy enough to solve. The number of sub problems always depends on the problem scenario.

• Conquer : Solving the sub problems recursively

• Combine : Combine the solutions of sub problems to generate solutions to the original problem.

As Divide and Conquer algorithm is a recursive approach, it is important to have what are the base cases for the given problem, on the basis of base cases only the given problem is divided into sub problems to find the solution.

Examples

Divide and Conquer algorithm is one of the most efficient algorithms used to solve many complex problems. But here to understand the approach more clearly, let us solve a simple problem which is "finding max element in an array". The problem can be solved in many ways, but in this post we cover how to solve using the divide and conquer approach.

Example1 : Max Element In An Array

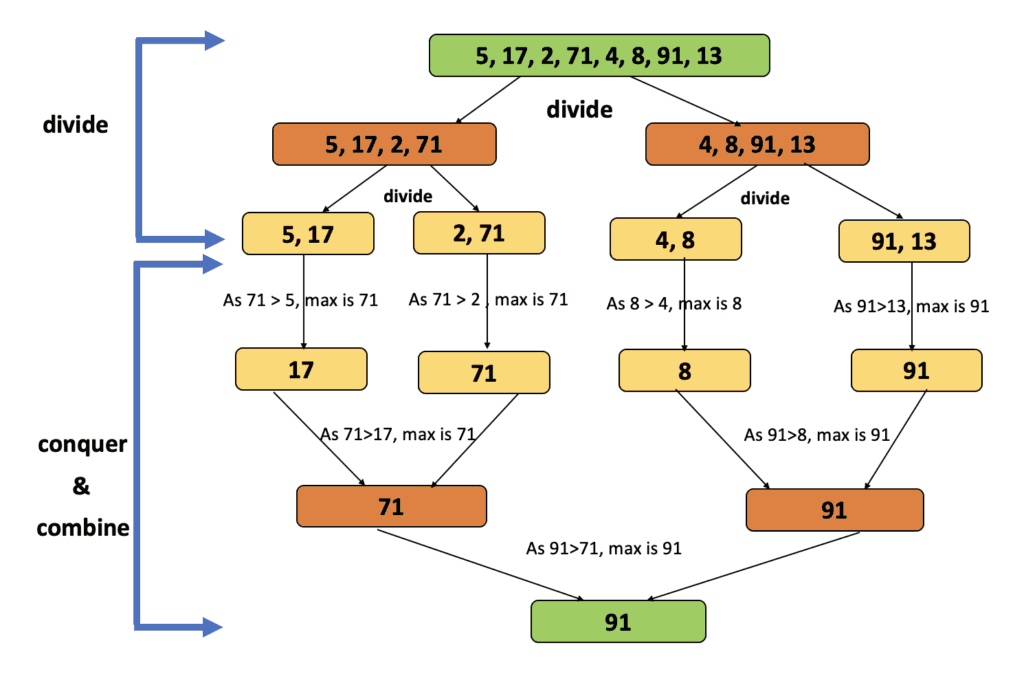
1Problem Description : Given an array A[] of size n (n > 0) , find the maximum element present in the array. 
2
3Constraints: The algorithm should make the minimum number of comparisons.
4
5Input: { 5, 17, 2, 71, 4, 8, 91, 13 }
6
7Output: 91

Solution Approach

• Divide step : Divide the array into two equal sub problems of the same size. i.e divide the array at mid index of the array and the two sub problems referred as left part and right part.
• Conquer step : Recursively find the maximum element in both left and right parts.
• Combine step : Compare maximum elements of both left and right parts to get the maximum element.
• Base cases :
  • If array size is 1, return the element
  • If array size is 2, compare two elements in the array and return max element.

1Input : int[] a of length n
2
3Step 0: Initialize start as 0 and end as n-1 (where n is length of the given array)
4
5Step 1: compute mid as mid = (start+end)/2 
6        to split the array into two halves.(Divide step)
7
8Step 2: recursively calculate max of two sub arrays which formed in step1. 
9        (Conquer step) 
10
11Step 3: find the max by comparing the max element of both halves
12
13Output : max element of the given array

Explanation

• Divide Step : Divide the array into two halves. Continue the process until the sub problems reach base conditions
• Conquer Step: As the sub problem reached one of base conditions means we can compute the solution which is maximum element of the sub problem
• Combine Step: Compare maximum of both left and right parts

Input : {5, 17, 2, 71, 4, 8, 91, 13}, n = 8

Initialization : start = 0 and end = 7 (n-1)

• Divide Steps :

  • start = 0 and end = 7 it means elements consider at this step are {5, 17, 2, 71, 4, 8, 91, 13}
  • compute mid as mid = (start+end)/2 = 3
  • It means the left sub array contains {5, 17, 2, 71} with start index at 0 and end index at 3 and right sub array contains {4, 8, 91, 13} with start index at 4 (mid+1) and end index at 7.
  • Now we have two sub problems from the original array. For both sub problems the same procedure continues until the sub problems reach one of the base conditions, for example a sub array of size having either 1 or 2.

• Conquer Steps:

  • Finding a maximum in an array of size 1 or 2 is pretty easy.
  • if array size is 1 return the element which is in the array
  • if array size is 2, compare both and return the maximum element among the two elements in the array

• Combine Steps:

  • From each sub problem we get one max element, we get two maximums one from the left part and the other from the right part based on the mid index which is computed.
  • So the combined array maximum element will be the one which is the maximum element of both left and right parts.

Code Implementation

1public class FindMax {
2
3    public int findMax(int[] input){
4        return findMax(input, 0, input.length-1);
5    }
6
7    // recursive method to calculate max element in given array
8    private int findMax(int[] input, int start, int end) {
9        
10        // Base case 1: if only one element in array
11        if(start == end) {
12            return input[start];
13        }
14
15        // Base case 2: if only two elements in the array
16        if(start+1 == end) {
17            return max(input[start], input[end]);
18        }
19
20        // calculate mid
21        int mid = start + (end - start) / 2 ;
22
23        // find max element of left sub array
24        int maxLeft = findMax(input, start, mid);
25
26        // find max element of right sub array
27        int maxRight = findMax(input, mid+1, end);
28
29        // compare max of both left and right parts
30        return max(maxLeft, maxRight);
31    }
32
33    // utility method to find max of two numbers
34    private int max(int num1, int num2){
35        if(num1 > num2) {
36            return num1;
37        }
38        return num2;
39    }
40
41    // Driver method
42    public static void main(String[] args) {
43        FindMax obj = new FindMax();
44        int[] input = { 5, 17, 2, 71, 4, 8, 91, 13};
45        System.out.println(obj.findMax(input));
46    }
47}

Complexity Analysis

Define recursive relation to understand the complexity of the approach. Consider T(n) is the time complexity of a given problem of size n.

• Every time we are dividing the problem into two equal sub problems of size n/2.
• Once we get the solution of sub problems (left and right parts), we are comparing the solution which takes 2 comparisons.
• During Base case scenarios, if n = 1 no comparisons and if n=2 we make 1 comparison to get the desired solution.

1T(n) = T(n/2) + T(n/2) + 2 = 2 T(n/2) + 2 where T(2) = 1 and T(1) = 0 
2By solving this relation using recursive tree method
3if n is power of 2, T(n) = 3*n/2 - 2

Time Complexity : O(n)

• If n is power of 2, it takes 3n/2 – 2 comparisons
• if n is not power of 2, > 3n/2 – 2 comparisons

Space Complexity : O(log n)

Recursive call stack uses O(log n) extra space.

Applications

• Maximum and Minimum Problem
• Binary Search
• Sorting (Merge Sort and Quick Sort)
• Tower of Hanoi
• Closest Pair of Points
• Karatsuba Algorithm
• Strassen’s Matrix Multiplication
• Cooley-Tukey Fast Fourier Transform Algorithm

Advantages and Disadvantages

Advantages

• Solving difficult problems : It is a powerful approach to solve difficult problems.
• Efficiency : It is an efficient approach in terms of number of operations when compared to brute force approach.
• Parallelism : It does not involve any modification and is handled by systems incorporating parallel processing.
• Memory access : It uses cache memory efficiently.

Disadvantages

• As it is a recursive approach, it always uses a recursive call stack which needs extra memory.
• System Crash : if the recursion is performed rigorously greater than the stack present in the CPU, it leads to crashing the system.