Introduction

Selection Sort Algorithm works by finding the minimum element of the array and placing the min element at its correct position. In the selection sort, the first element is selected as minimum and visits other elements of the array, If any element is found lesser than the current minimum, the minimum value gets updated. This process gets repeated for other elements of the array.

Algorithm

1Step 0 : Initialize n to length of the array
2
3Step 1 : Initialize j to 0 and compare a[j] with a[j+1] 
4         (compare adjacent elements starting from 0th index)
5
6Step 2 : if a[j] > a[j+1] swap a[j] and a[j+1]
7
8Step 3 : repeat steps 1 and 2 until j reached end of the array 
9         (by end of this one element will be placed at its correct order)
10
11Step 4 : continue from Step 1 n-1 times 
12         (so that all elements will be in proper order)

Example Explanation

1Input array : a = {5, 3, 13, 2, 11, 4, 7} 

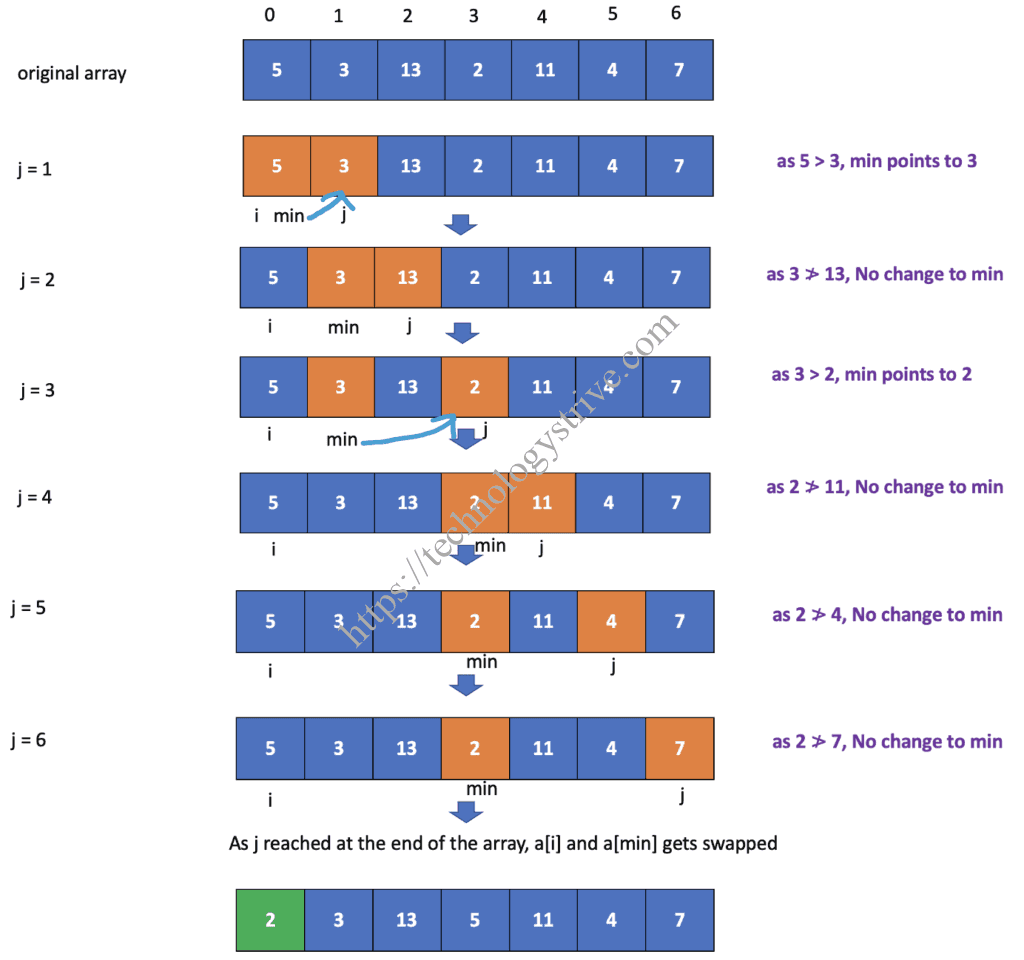
Iteration 1 : (i = 0)

Step 1 : Initialize i = 0

Step 2: Initialize min to i and j = i+1 So min = 0 and j = 1.

Step 3: Compare a[min] with a[j] & change min index if a[min] > a[j]

Step 4: Increment j & repeat from Step 3 until j reaches end of the array.

Iteration 2 : (i = 1)

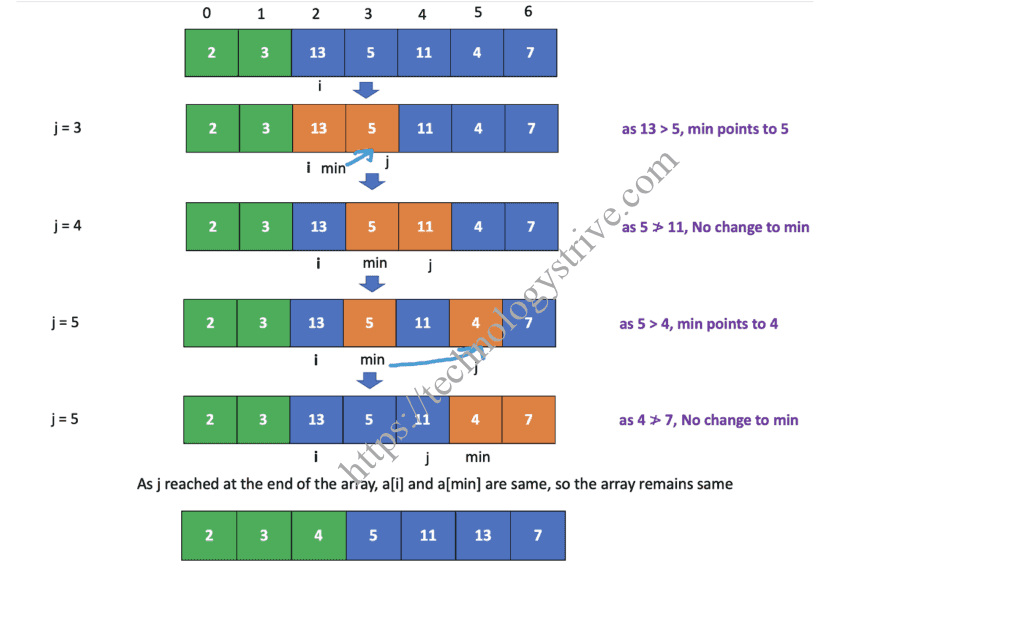
Iteration 3 : (i = 2)

Iteration 4 : (i = 3)

Iteration 5 : (i = 4)

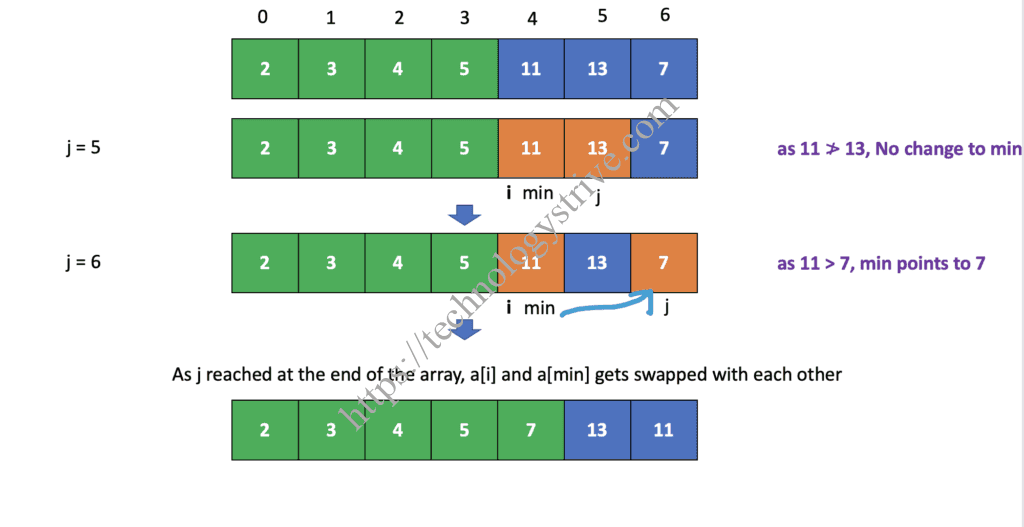
Iteration 6 : (i = 5)

Implementation

1public class SelectionSort {
2
3    // Method to sort a given array
4    public void sort(int[] array) {
5        int n = array.length;
6        for(int i=0;i<n-1;i++){
7            // Let us assume a[i] is the smallest element of unsorted array
8            // initialize min index with i
9            int min = i;
10
11            for(int j=i+1;j<n;j++){
12                // compare a[min] with a[j] and change min index accordingly
13                if(array[min] > array[j]){
14                    // as array[min] is greater that current element, update min index with j
15                    min = j ;
16                }
17            }
18            // at the end of the iteration we know what is min of the unsorted array
19            // swap elements at min and i
20            // it means element at i is part of sorted array
21            // continue same process for remaining un sorted array
22            swap(array, i, min);
23            // if you want to see the array at the end of every iteration, uncomment below lines
24            // System.out.println("Iteration "+i);
25            // print(array);
26        }
27    }
28
29    // method swap values at index i and j of array
30    private void swap(int[] array, int i, int j){
31        int temp = array[i];
32        array[i] = array[j];
33        array[j] = temp;
34    }
35
36    // Helper method to print an array
37    private void print(int[] array) {
38        for(int i=0; i<array.length; i++) {
39            System.out.print(array[i]+"\t");
40        }
41        System.out.println();
42    }
43
44    // Driver Code
45    public static void main(String[] args){
46        int[] a = {5, 3, 13, 2, 11, 4, 7};
47        SelectionSort obj = new SelectionSort();
48        obj.print(a);
49        obj.sort(a);
50        obj.print(a);
51    }
52}

Complexity Analysis

• Time Complexity : O(n^2).
• Space Complexity : O(1) .